
About This Course
The Probability and Statistics course provides an essential introduction to data analysis tools, which are indispensable in engineering studies. It enables learners to understand how to collect, organise, analyse and interpret data from real-life situations related to industrial processes. This course provides them with the necessary foundations for modelling phenomena, assessing uncertainties and basing their technical decisions on rigorous analysis. It thus plays a fundamental role in their ability to exploit experimental data and improve the performance of the systems and processes they will encounter throughout their careers.
Targeted Competencies
Fundamentals of probability and statistics
Data classification
Calculation of descriptive statistics
Decision-making and prediction
Requirements
Master basic mathematical concepts
Solve simple mathematical problems
Apply basic logic and reasoning
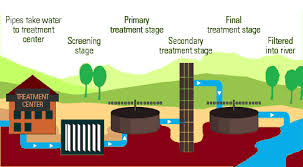
This three-year engineering program specializes in Water Treatment Technology and Sustainable Water Resource Management (TTEE), equipping students to address critical challenges such as water scarcity, quality degradation, and environmental impacts. Graduates develop multidisciplinary expertise in engineering, chemistry, biology, and water systems management, enabling them to effectively address environmental, industrial, and societal water-related challenges.
- ---Be introduced to basic technical terms related to water treatment and operations.
- ---Understand the importance of technical English in their field.
- ---Improve skills in technical writing, communication, and presentation
- ---Gain confidence in discussing water treatment technologies and innovations
- Enseignant: bechohra louiza bechohra louiza

On completion of this module, 2nd year engineering-process engineering students will be able to identify occupational hazards and risks, assess their severity and probability of occurrence, implement appropriate preventive measures and monitor the effectiveness of the safety measures put in place. They will also be able to identify how to prevent occupational accidents and illnesses, and promote a safety culture within a company.
- Enseignant: IKEZRANE KEZRANE Imane